Bei deutschen Lebensversicherungspolicen handelt es sich in aller Regel um langfristige Verträge, die eine durchschnittliche Laufzeit von weit über 20 Jahren aufweisen. Der Versicherungsnehmer verbindet mit dem Abschluss eines solchen Vertrages die Erwartung, für sein Alter in angemessener Form vorsorgen zu können. Die individuelle Bedarfssituation des Versicherungsnehmers kann sich aber im Laufe der Zeit deutlich verändern. Es war und ist daher für ein Versicherungsunternehmen unerlässlich, seine Produkte durch Optionsrechte aufzuwerten, die es dem Versicherungsnehmer ermöglichen, den Versicherungsschutz zukünftig an aktuelle Gegebenheiten anzupassen. Optionen und Garantien spielen daher in der Lebensversicherung eine ganz zentrale Rolle.
Beispiele für solche Finanzoptionen sind:
- Kündigung
- Beitragsfreistellung und -wiederaufnahme
- Teilauszahlungsoption
- Freiwillige Zuzahlung
- Abrufoption
- Kapitalwahlrecht
- Aufschub- und Verlängerungsoption
- Erhöhung der Versicherungssumme
Die Ausübung von Optionen stellt für das Versicherungsunternehmen ein finanzielles Risiko dar, da sie die zukünftigen Zahlungsströme erheblich beeinflussen können. Diese Risiken werden jedoch bisher in den wenigsten Fällen explizit in der Produktkalkulation berücksichtigt. Dies liegt vor allem daran, dass die Einflussfaktoren auf die Ausübung von Optionen vielfältig sind und die exakte Berechnung des Optionswertes nicht trivial ist. So spielen neben der aktuellen Kapitalmarktsituation und der Höhe der Überschussbeteiligung auch die persönlichen Bedürfnisse und die aktuelle Vertragssituation eine entscheidende Rolle.
Aus finanzmathematischer Sicht entspricht der Wert der Option den Kosten der Absicherung am Kapitalmarkt. Dafür gibt es eine Reihe von Methoden, die zur Bewertung herangezogen werden können (z.B. Monte-Carlo-Simulation). Ihre Komplexität und die Notwendigkeit stochastischer Simulationen zeigen den Unternehmen aber oftmals Grenzen ihrer Bewertungsmöglichkeiten auf.
Neben den Vertragsoptionen bietet die klassische deutsche Lebensversicherung ihren Kunden derzeit einen Garantiezins von 1,75 % bzw. 1,25 % ab 01.01.2015 auf den Sparbeitrag. Dieses Modell ist in Europa nur noch selten zu finden. In den meisten anderen Ländern gibt es solche Garantien gar nicht mehr, dort tragen die Kunden das gesamte Kapitalanlagerisiko.
Optionen und Garantien unter Solvency II
Solvency II basiert auf einer Marktwertbetrachtung. Im Rahmen der Ermittlung des Best Estimates der versicherungstechnischen Verpflichtungen ist es daher unabdingbar, in den zukünftigen Zahlungsströmen auch Optionen und Garantien der Versicherungsnehmer zu berücksichtigen. Optionen können den Verlauf der Zahlungsströme maßgeblich beeinflussen und rufen so mitunter Kosten hervor, die zu Lasten des Versichertenbestandes gehen. Insbesondere zu Lasten derer, die ihr Wahlrecht nicht zu ihren Gunsten nutzen oder gar keines besitzen. Dieses implizite Risiko ist mit entsprechend hohem Eigenkapital zu hinterlegen. Gleiches gilt für die Garantien. Auch für sie ist nach den neuen Regeln Solvenzkapital vorzuhalten.
Es wird erwartet, dass die klassische deutsche Lebensversicherung mit ihrer Zinsgarantie vor dem Hintergrund von Solvency II unter Druck gerät. Dabei bleibt abzuwarten, ob das deutsche Modell dem erhöhten Kostendruck Stand halten kann, oder in wieweit Versicherungsunternehmen ihre Produktgestaltung anlässlich des neuen Regelwerks überdenken werden
Vereinfachende Ansätze zur Ermittlung der Optionen und Garantien
Der GDV hat im Rahmen seiner Brückentechnolgie vereinfachende Verfahren zur Ermittlung des Wertes der in Versicherungsverträgen enthaltenen Optionen und Garantien vorgestellt. Dabei werden die Optionen mit Hilfe eines von der DAV-Arbeitsgruppe „Reservierung von Garantieprodukten“ vorgeschlagenen Zinsabschlagsverfahrens ermittelt. Der Wert der Garantien wird als Wert einer Austauschoption modelliert, welcher über eine Verallgemeinerung des Black-Scholes-Ansatzes mit einer geschlossenen Formel ermittelt werden kann.
Bewertung der Optionen
Seitens des GDV werden zur Bestimmung des Wertes der Optionen der Versicherungsnehmer zwei zentrale Vertragsoptionen zur Approximation berücksichtigt:
- garantierter Rückkaufswert (gRKW)
- Kapitalwahlrecht (KWR)
- modelliert als Kapitalversicherung (-K)
- modelliert als Rentenversicherung (-R)
Basis für die Durchführung des Zinsabschlagsverfahrens bilden die Anteile, die die Verträge mit den oben genannten Optionen am Gesamtbestand haben. Durch Multiplikation dieser Anteile mit vorgegebenen Zinsabschlagsfaktoren ergibt sich der unternehmensindividuelle Zinsabschlag
Die aktuellen Zinsabschläge (Stand: LTGA 2013) beziffern sich je Versicherungsnehmeroption auf:
| Zinsabschlag | Best Estimate | Zins- anstieg | Zins- rückgang |
|---|---|---|---|
| gRKW | 2,4 bp | 13,4 bp | 0,6 bp |
| KWR - K | 15,2 bp | 4,8 bp | 25,6 bp |
| KWR – R | 1,0 bp | 5,6 bp | 0 bp |
| gRKW + KWR - K | 16,2 bp | 16,2 bp | 25,4 bp |
| gRKW + KWR - R | 1,8 bp | 13,4 bp | 0 bp |
Die Berechnung des Erwartungswerts der garantierten Leistungen erfolgt dann zum einen mit der ursprünglichen risikofreien Zinsstrukturkurve (vgl. (vgl. Bewertung versicherungstechnischer Verpflichtungen) und zum anderen mit der um den errechneten Zinsabschlag modifizierten Zinsstrukturkurve. Der Wert der Versicherungsnehmeroption pro Szenario entspricht dann der Differenz dieser beiden Erwartungswerte.
Bewertung der Garantien
Zur Bestimmung des Wertes der Garantien wird auf eine Verallgemeinerung des Black-Scholes-Modells zurückgegriffen. Dabei wird der Wert der Garantie als Wert der Austauschoption zwischen zwei Portfolien A und B modelliert. Portfolio A umfasst dabei die garantierten Leistungen, während Portfolio B all die Kapitalanlagen enthält, die zur Bedeckung der versicherungstechnischen Verpflichtungen dienen (Garantieleistungen zuzüglich der zukünftigen Überschüsse für Versicherungsnehmer). Als vereinfachende Annahme werden alle Kapitalanlagen den drei Kategorien Aktien, Immobilien sowie festverzinslichen Wertpapieren zugeordnet und deren Anteil am Gesamtportfolio berechnet
Anschließend werden die Werte und Volatilitäten der Portfolien A und B unter Zuhilfenahme einer Reihe (vorgegebener) Marktparameter berechnet und die Korrelation ρ zwischen den beiden Portfolien ermittelt. Der Wert der Austauschoption – und damit der Wert der Garantien – ergibt sich dann als
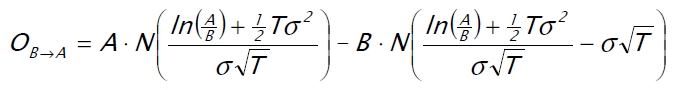 ,
,
wobei σ die Volatilität der Differenz von A und B beschreibt und sich aus den Volatilitäten der Portfolien ergibt. Es gilt
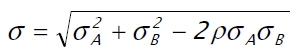 .
.