Mit der legislativen Umsetzung des Solvency II-Projekts Anfang 2016 in den Ländern der Europäischen Union sind einige wesentliche Änderungen der jeweiligen nationalen Versicherungsaufsichtsgesetze verbunden. Ein neuer Aspekt ist hierbei die Vorschrift, potenzielle Abweichungen des Risikoprofils des Unternehmens von den Annahmen, die der Standardformel zur Berechnung des Solvency Capital Requirements (SCR) zugrunde liegen, zu analysieren und zu beurteilen. Für das Prämien- und Reserve-Risiko bzw. die zugehörigen Schaden-Kosten-Quoten wird dabei stillschweigend eine Lognormal-Verteilung unterstellt. In diesem Beitrag wird ein einfaches, aber dennoch mathematisch korrektes Verfahren auf der Basis von Quantil-Quantil-Plots vorgestellt, mit dem eine solche Analyse durchgeführt werden kann.
Vorbemerkung
In § 27 des neuen deutschen Versicherungsaufsichtsgesetztes heißt es: Zum Risikomanagementsystem gehört eine unternehmenseigene Risiko- und Solvabilitätsbeurteilung, die Versicherungsunternehmen regelmäßig sowie im Fall wesentlicher Änderungen in ihrem Risikoprofil unverzüglich vorzunehmen haben. … Die Risiko- und Solvabilitätsbeurteilung umfasst mindestens
- eine eigenständige Bewertung des Solvabilitätsbedarfs unter Berücksichtigung des spezifischen Risikoprofils, der festgelegten Risikotoleranzlimite und der Geschäftsstrategie des Unternehmens,
- eine Beurteilung der jederzeitigen Erfüllbarkeit der aufsichtsrechtlichen Eigenmittelanforderungen, der Anforderungen an die versicherungstechnischen Rückstellungen in der Solvabilitätsübersicht und der Risikotragfähigkeit sowie
- eine Beurteilung der Wesentlichkeit von Abweichungen des Risikoprofils des Unternehmens von den Annahmen, die der Berechnung der Solvabilitätskapitalanforderung mit der Standardformel oder mit dem internen Modell zugrunde liegen.
Konkret geht es hierbei um die Annahme einer Lognormal-Verteilung für das Prämien- und Reserve-Risiko bzw. für die jährlichen Schaden- bzw. Schaden-Kosten-Quoten. Eine mathematisch korrekte Überprüfung dieses Sachverhalts kann eigentlich nur mit geeigneten statistischen Tests durchgeführt werden. In diesem Beitrag wird ein neues Formelwerk vorgestellt, mit dem diese Annahme mit Hilfe von Quantil-Quantil-Plots leicht überprüft werden kann. Quantil-Quantil-Plots haben darüber hinaus den Vorteil, die Testergebnisse auch graphisch veranschaulichen zu können, was insbesondere mathematisch weniger geschulten Mitarbeitern von Versicherungsunternehmen entgegenkommen dürfte.
Einführung
Graphische Methoden zur statistischen Analyse und Parameterschätzung in Lage-Skalen-Familien von Wahrscheinlichkeitsverteilungen haben eine lange Traditition, sie gehen auf sogenannte „Wahrscheinlichkeitspapiere“ (Quantil-Quantil-Plots) zurück, die etwa ab dem Beginn des 20. Jahrhunderts vor allem im ingenieurwissenschaftlichen Kontext zur Anwendung kamen. Lag der Schwerpunkt zunächst auf der Anpassung der Normalverteilung an hydrologische Beobachtungen, kamen später insbesondere Anpassungen an Extremwertverteilungen und andere Klassen von Wahrscheinlichkeitsverteilungen hinzu. Eine „optimale“ Wahl der Plot-Positionen (auf der Abszisse) ist dabei eng verbunden mit der Berechnung von Erwartungswerten der geordneten Beobachtungen (sog. Ordnungsstatistiken).
Später wurden die üblichen Schätzverfahren für Lage- und Skalenparameter um geeignete Testverfahren erweitert, mit denen unabhängig von diesen Parametern das Vorliegen eines bestimmten Verteilungstyps überprüft werden kann. Ein interessanter Zugang besteht hier in der Verwendung einer geeigneten Transformation des empirischen Korrelationskoeffizienten aus dem Quantil-Quantil-Plot als Testgröße.
Quantil-Quantil-Plots und Lage-Skalen-Familien
Betrachtet werden Risiken X der Form X = μ + σ Z mit einem „Prototypen“ Z und stetiger, streng monotoner Verteilungsfunktion FZ (Lage-Skalen-Familie mit dem reellen Lageparameter μ und dem positiven Skalenparameter σ). Ziel ist einerseits die Schätzung der Parameter μ und σ sowie andererseits die Überprüfung der Verteilungshypothese anhand von n Beobachtungen. Bezeichnet dazu X(k) die k-te Ordnungsstatistik (d.h. den k-größten Wert) aus einer Reihe von unabhängigen Replikationen X1,…,Xn von X, so trägt man im Quantil-Quantil-Plot die Größen (QZ (uk), X(k)) mit der Quantilfunktion QZ = FZ–1 und geeigneten uk , k = 1, …,n ab und ermittelt mittels üblicher linearer Regression die Ausgleichsgerade mit Achsenabschnitt μ* und Steigung σ*.
Die Bedeutung der Erwartungswerte der Ordnungsstatistiken für die Parameterschätzungen zeigt sich in der folgenden
Proposition 1: Mit der Wahl uk = FZ(E(Z(k))) für k = 1, …,n sind μ* und σ* erwartungstreue Schätzer für μ und σ.
Im Kontext von Solvency II (Säule I) werden die Schaden- bzw. Schaden-Kosten-Quoten als lognormalverteilt angenommen. Die entsprechenden logarithmierten Größen sind dann normalverteilt, so dass hier die Bestimmung bzw. numerische Berechnung der Erwartungswerte der Ordnungsstatistiken der Standard-Normalverteilung relevant ist. Diese sind aber leider nicht elementar berechenbar. Umfangreiche numerische Auswertungen für E(Z(k)) wurden von Harter (1961) publiziert. In der Literatur findet man dazu zahlreiche numerische Approximationen in der Form E(Z(k)) ≈ Φ–1(uk) mit der üblichen Bezeichnung Φ für die Verteilungsfunktion der Standard-Normalverteilung, z.B.
| Hazen (1914) | uk = (k – 0,5)/(n + 1) |
| Weibull (1939) | uk = k /(n + 1) |
| Beard (1943) | uk = (k – 0,31)/(n + 0,38) |
| Benard and Bos-Levenbach (1953) | uk = (k – 0,3)/(n + 0,2) |
| Blom (1958) | uk = (k – 0,375)/(n + 0,25) |
| Tukey (1962) | uk = (k – 0,333)/(n + 0,333) |
| Gringorten (1963) | uk = (k – 0,44)/(n + 0,12) |
Aus einer größeren Monte-Carlo-Studie ergibt sich als sehr gute Approximation für die uk dagegen
uk = (k – an)/(n + bn),
wobei
an = 0,27950585 + 0,04684273/(0,34986981 + n–0,79499457)
bn = 0,44480354 – 0,09890767/(0,36353365 + n–0,78493983)
für 1 ≤ k ≤ n ≤ 100.
Durch Vergleich mit den Werten aus der obigen Tabelle ergibt sich eine sehr gute Übereinstimmung zu Blom (1958) für n = 12 und zu Tukey (1962) für n = 2. Die übrigen Approximationsformeln weisen demgegenüber größere Abweichungen auf.
Quantil-Quantil-Plots und Lage-Skalen-Familien: Tests
Es gibt in der Literatur eine Reihe von Vorschlägen zum Testen der Hypothese
H0: die Verteilung des Risikos X entstammt der Lage-Skalen-Familie zu Z
(sog. einfacher Signifikanz-Anpassungstest). Interessant sind hier Tests auf der Basis des empirischen Korrelationskoeffizienten ρn aus dem Quantil-Quantil-Plot (Erwartungswerte der Ordnungsstatistiken vs. den der Größe nach angeordneten Beobachtungswerten). Die Tatsache, dass die Verteilung des empirischen Korrelationskoeffizienten unter der Nullhypothese von den Lage- und Skalenparametern unabhängig ist, folgt aus der folgenden
Proposition 2: Sind S und T zwei Risiken mit endlicher Varianz, so gilt für die Korrelation
Korr(aS + b, cT + d) = Korr(S,T) für alle rellen a,b,c,d mit a×c > 0.
In diesem Beitrag schlagen wir eine geringfügige Modifikation als Teststatistik vor, nämlich Tn := – ln(1 – ρn). Dies hat den Vorteil, dass die Verteilung von Tn unter der Nullhypothese einer Normalverteilung für Werte von n ≥ 10 recht gut selbst durch eine Normalverteilung approximiert werden kann, so dass sich die p-Werte für den Anpassungstest einfach, z.B. mit EXCEL, berechnen lassen.
Die Parameter μn und σn der angepassten Normalverteilung für die Teststatistik lassen sich im Bereich n = 10, …,50 recht gut durch folgende Interpolation approximieren:
μn ≈ (5,87383n + 101,011)/(n + 35,3404)
σn ≈ (0,477812n + 3,25495)/(n + 2,72721).
Fallstudie
In diesem Abschnitt werden die im vorigen Teil beschriebenen Verfahren anhand von Informationen aus der Versicherungsbranche veranschaulicht. Konkret geht es um brutto-Schaden-Kosten-Quoten der Sparten Sach gesamt, Sach privat, verbundene Gebäudeversicherung (VGV), verbundene Hausratversicherung (VHV), Unfall, Rechtsschutz, Gewerbe und allgemeine Haftpflicht. Die Daten wurden dem vom GDV herausgegebenen Statistischen Taschenbuch der Versicherungsbranche (2018) ab dem Jahr 2000 entnommen (Haftpflicht ab 2004). Es soll geprüft werden, ob die Schaden-Kosten-Quoten lognormal-, also die logarithmierten Quoten normalverteilt sind. Der jeweilige Quantil-Quantil-Plot wird deshalb mit den logarithmierten Quoten erstellt. Die Nullhypothese lautet hier: die (logarithmierten) Quoten sind normalverteilt. Angegeben sind der jeweilige Wert der Teststatistik sowie der zugehörige (approximative) p-Wert.
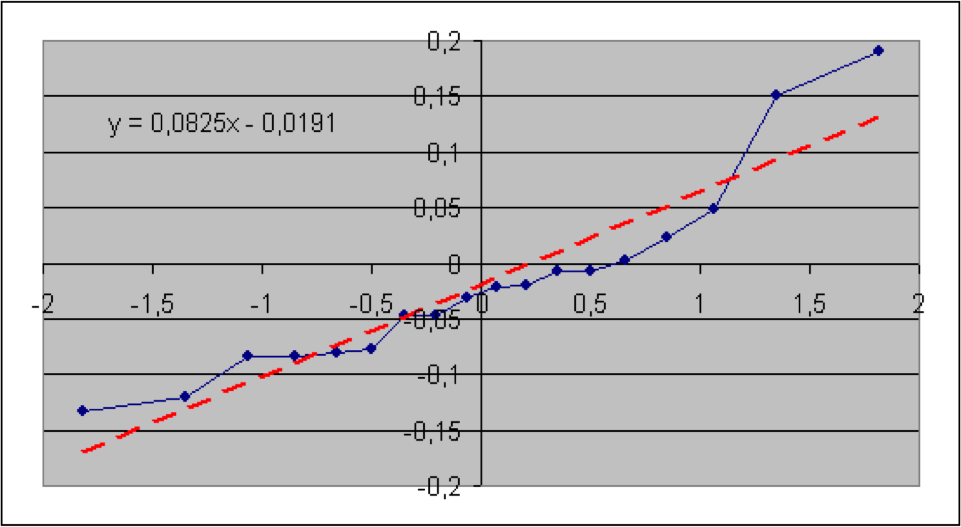
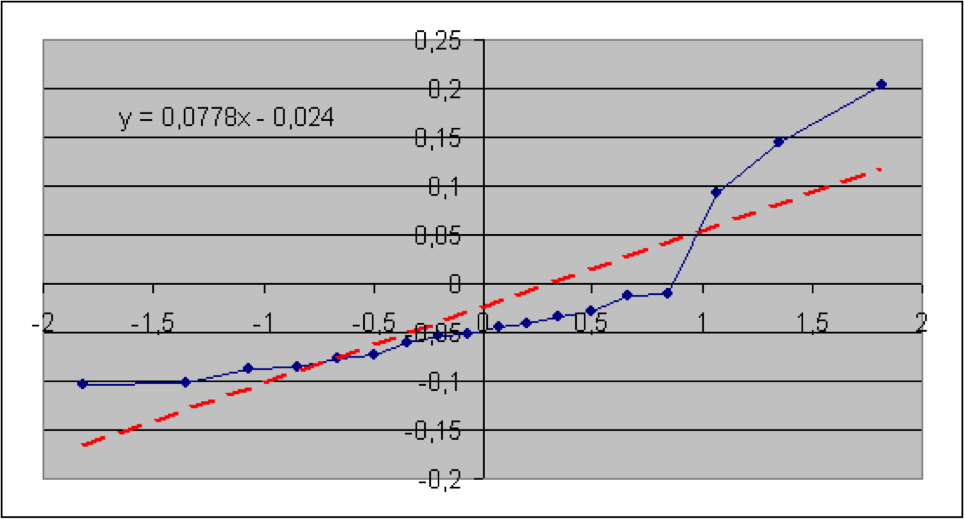
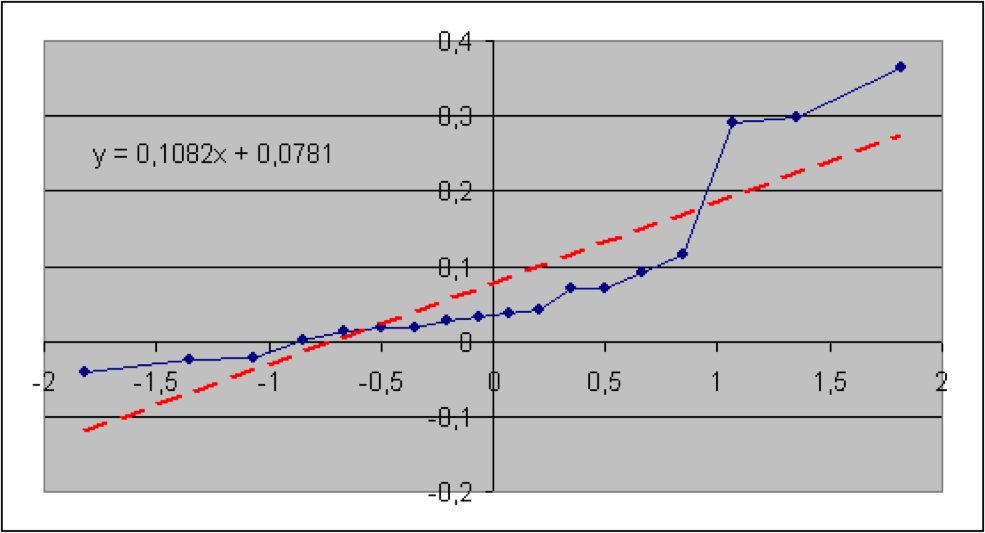
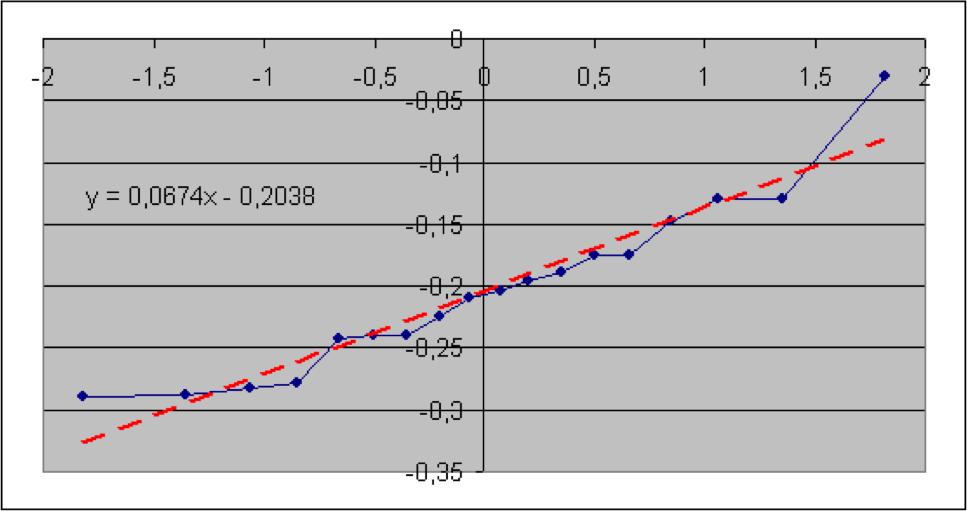
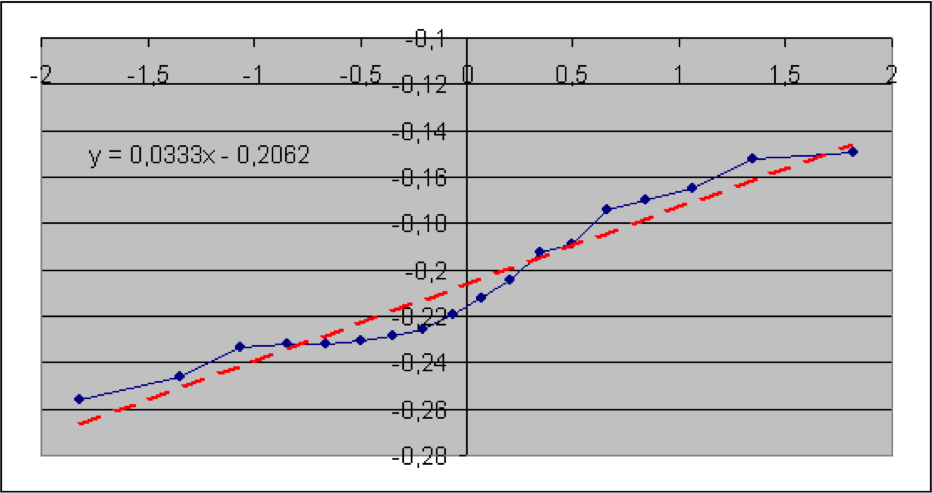
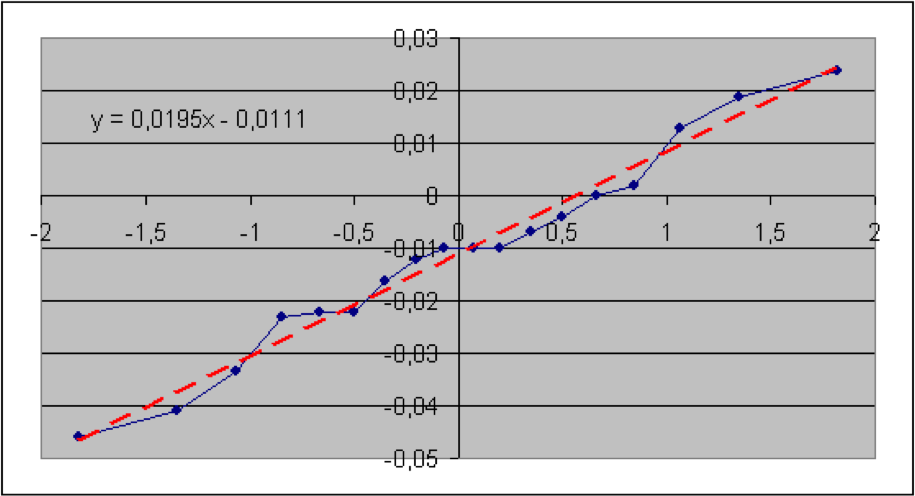
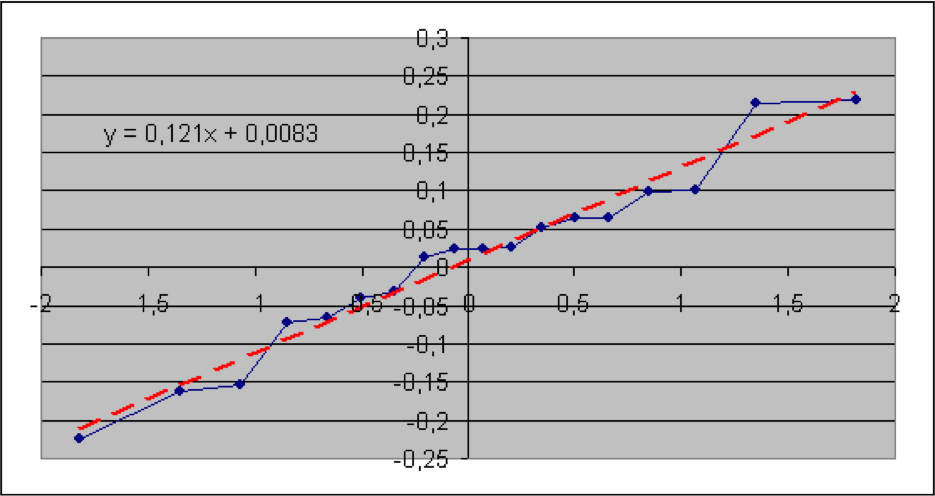
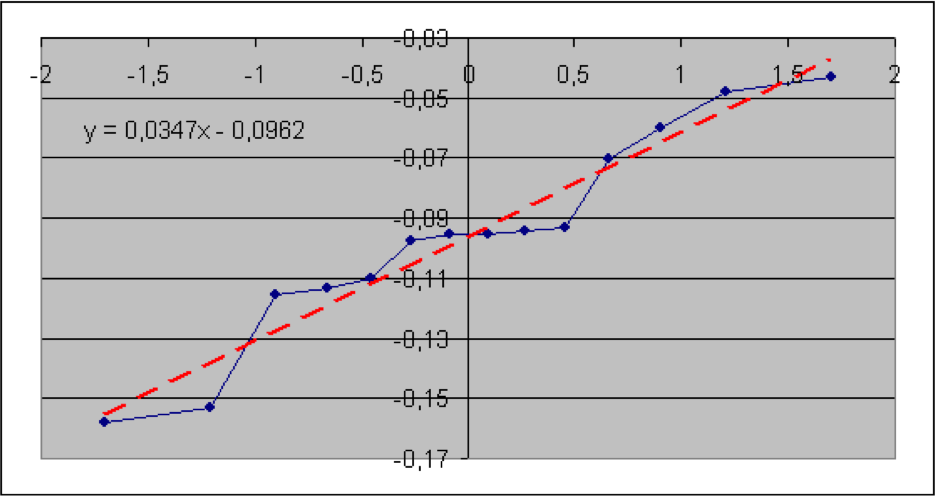
Es zeigt sich, dass hier die p-Werte der Sparten Sach privat und VGV extrem niedrig ausfallen, so dass die Nullhypothese einer Lognormal-Verteilung für die Schaden-Kostenquoten aus statistischen Gründen abzulehnen ist. Bei der Sparte Sach gesamt würde die Nullhypothese bei einer Fehlerwahrscheinlichkeit 1. Art von 5% knapp abgelehnt. Bei den Sparten VHV, Unfall, Rechtsschutz, Gewerbe und allgemeine Haftpflicht wird die Nullhypothese bei einer Fehlerwahrscheinlichkeit 1. Art selbst von 15% nicht verworfen.
Als geschätzte Parameter für die Normal- (bzw. Lognormal-Verteilung) erhält man jeweils aus dem Achsenabschnitt die Größe μ* und aus der Steigung die Größe σ*.
Fazit
Ein Korrelationstest auf der Basis von Quantil-Quantil-Plots ist einfach durchzuführen und hat gegenüber anderen Anpassungstests den Vorteil, explizit näherungsweise gute p-Werte aller Größenordnungen für beliebige Stichprobenumfänge zu erhalten. Empirische Studien zeigen dabei eine vergleichbare Güte zu alternative Testverfahren.
Quantil-Quantil-Plots bieten darüber hinaus den großen Vorteil einer graphischen Veranschaulichung der Testergebnisse, was insbesondere für mathematisch weniger geschulte Mitarbeiter von Versicherungsunternehmen interessant sein dürfte.
Schlussbemerkung
Bei diesem Beitrag handelt es sich um eine Kurzfassung der Arbeit
D. Pfeifer: Modellvalidierung mit Hilfe von Quantil-Quantil-Plots unter Solvency II,
Zeitschrift für die gesamte Versicherungswissenschaft (2019) 108: 307-325, https://doi.org/10.1007/s12297-019-00451-y
Die im obigen Beitrag angegebenen Referenzen sind dort ausführlich dokumentiert.
Literatur
- Cunnane, C.: Unbiased plotting positions - a review. Journal of Hydrology 37, 205–222 (1978)
- Czado,C., Schmidt, T.: Mathematische Statistik. Springer, Berlin (2011)
- Dallal, G.E., Wilkinson, L.: An analytic approximation to the distribution of Lilliefors’s test statistic for normality. In: The American Statistician 40, 294–295 (1986)
- David, H.A., Nagaraja, H.N.: Order Statistics. Wiley, N.Y. (2003)
- Dreher, M. (Hrsg.): Beck’sche Kurzkommentare: Prölss/Dreher: Versicherungsaufsichtsgesetz mit Nebengesetzen. 13. Aufl., C.H. Beck Verlag, München (2018)
- Harter, H.L.: Expected values of normal order statistics. Biometrika 48, 151–165 (1961)
- Gesamtverband der Deutschen Versicherungswirtschaft (GDV): Statistisches Taschenbuch der Versicherungswirtschaft 2018. Verlag Versicherungswirtschaft, Karlsruhe (2018)
- Gumbel, E.J.: Statistics of Extremes. Columbia University Press, N.Y. (1958)
- Guo, S.L.: A discussion on unbiased plotting positions for the general extreme value distribution. Journal of Hydrology 121, 33–44 (1990)
- Lockhart, R.A., Stephens, M.A.: The probability plot: tests of fit based on the correlation coefficient. In: N. Balakrishnan und C.R. Rao (Hrsg.): Handbook of Statistics 17, Order Statistics: Applications, Elsevier Science, 453–473 (1998)
- Sachs, L., Hedderich, J: Angewandte Statistik. Methodensammlung mit R. 12. Aufl., Springer, Berlin (2006)
- Weibull, W.: A statistical theory of strength of materials. Ing. Vet. Ak. Handl. (Stockholm), 151 (1939)