Solvenzkapitalanforderungen am Beispiel des Datenmodells der „IVW Privat AG“ – Teil 3

Kleinere und mittlere Unternehmen können dabei ihre Solvenzkapitalanforderungen mit Hilfe der Standardformel ermitteln, deren Funktionsweise für ein Schadenversicherungsunternehmen in den beiden vorangegangenen Teilen mit Hilfe des Datenmodells der sogenannten „IVW Privat AG“ erläutert worden ist. ¹

Alternativ zur Standardformel können die Kapitalanforderungen aber auch mit Hilfe eines internen Modells gerechnet werden, welches aufgrund des hohen Aufwands wohl aber eher nur für größere Unternehmen in Frage kommt

Daher wird zum Vergleich mit der Standardformel in diesem Teil für das Datenmodell der IVW Privat AG die Konzeption eines internen Modells skizziert, wobei mit einer zur Standardformel analogen Parametrisierung gearbeitet wurde, so dass die Unterschiede nicht in einer geänderten

(individualisierten) Parameterwahl, sondern in der methodischen Vorgehensweise liegen. Eine detaillierte Darstellung der hier zusammengefassten Ergebnisse kann in der Publikationsreihe „Forschung am IVW Köln“ heruntergeladen werden. ²

Beim internen Modell der IVW Privat AG ergibt sich das stochastische ökonomische Eigenkapital zum Ende der Bilanzperiode als

EK₁ (ω) := EK₀ + GuV₁ (ω)

mit EK₀ das deterministische ökonomische Eigenkapital zu Beginn der Bilanzperiode (in Höhe von 8.887 T€ für die IVW Privat AG) und GuV₁ (ω) eine stochastische Realisierung einer ökonomischen Gewinn- und Verlustrechnung in der Bilanzperiode, wobei sich die Gewinn- und Verlustrechnung klassisch aus einem versicherungstechnischen und einem nicht-versicherungstechnischen Teil zusammensetzt.

Analog zur Standardformel wurden in der Gewinn- und Verlustrechnung die Risikoeinflüsse von

• Markt- und Assetrisiken,
• Ausfallrisiken und immaterielle Risiken,
• Underwritingrisiken in Nichtleben und Kranken sowie
• operationelle Risiken

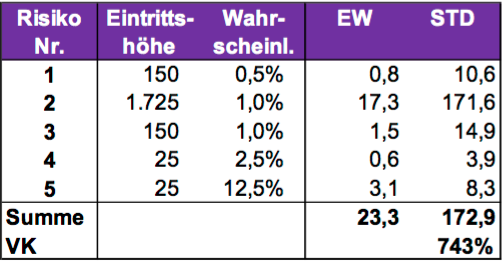
einbezogen. Bis auf die operationellen Risiken erfolgten alle Parametrisierungen und Modellierungen möglichst analog zur Standardformel. Die Modellierung der operationellen Risiken erfolgte analog zum Partialmodell der IVW Privat AG auf Basis der nachfolgenden Risikomatrix: ³

Abbildung 1: Risikomatrix der IVW Privat AG in T€.

Auf Basis dieser stochastisch modellierten originären Risikoeinflüsse wurde das versicherungstechnische Ergebnis der IVW Privat AG modelliert als

VT Ergebnis = Ergebnis aus Basisschäden

+ Ergebnis aus Nat Cat Schäden

+ Ergebnis aus Großschäden

sowie das nicht-versicherungstechnische Ergebnis als

NVT Ergebnis = Ergebnis aus Marktrisiken und immateriellen Risiken,

+ Ergebnis aus Ausfallrisiken

+ Ergebnis aus sonstigen Risiken.

Aus diesen beiden Positionen ergibt sich dann das Gesamtergebnis nach Anwendung des Ergebnisses aus Steuern, wobei sich das Ergebnis aus Steuern aus einem proportionalen Steuereffekt (durch Anwendung des unternehmensindividuellen Steuersatzes) und ggf. einem nicht-proportionalen Abschreibungseffekt (bei nicht werthaltigen aktiven latenten Steuern) ergibt.
Der Abschreibungsalgorithmus wurde hier analog zu dem Abschreibungsalgorithmus in der Standardformel gewählt.

Mit den gewählten Modellansätzen kann sowohl das Soll-Szenario (im Sinne einer deterministischen Kontrollrechnung) als auch das Ist-Szenario (im Sinne einer stochastischen Realisierung) aus den Fortschreibungsberechnungen mit dem Standardformelansatz reproduziert werden.

Das deterministische Kontrollszenario ist sinnvoll zur Verprobung der Erwartungswerte eines gesamten Simulationslaufes, da man mit einem Simulationsansatz niemals exakte Werte reproduzieren kann.

Bei einer ausreichend großen Anzahl von Simulationen ist die empirische Verteilung, die man auf Basis des Simulationslaufes erhält, eine gute Approximation für die unbekannte wahre Verteilung und kann daher zur Berechnung der Verteilungsparameter sowie zur Berechnung der Ruinwahrscheinlichkeit herangezogen werden, wobei in der nachfolgenden Tabelle für das interne Modell der IVW Privat AG der Vergleich zwischen den simulierten Erwartungswerten mit den Werten aus der deterministischen Kontrollrechnung illustriert ist. ⁴

Simulationslauf

Im Schnitt reproduziert der Simulationslauf ziemlich gut die deterministische Kontrollrechnung. Nur bei der nicht-proportionalen Abschreibung aktiver latenter Steuern tritt ein wesentlicher Unterschied auf, da dieser Effekt nicht deterministisch abgebildet werden kann

Aus der EK-Verteilung ergibt sich der Eigenkapitalbedarf zum Ablauf des Jahres als

EK-Bedarf = E [EK₁] – VaR _0,5% [EK₁]

= 9.444 – 4.850

= 4.594.

In diesem Wert sind sowohl die erwartete GuV als auch die im Modell angesetzte risikofreie Verzinsung in Höhe von 2,5% auf das Eigenkapital zu Beginn enthalten, so dass sich der Solvenzkapitalbedarf zu Beginn des Jahres als

SCR = 8.887 – 4.850 / 1,025

= 4.155

ergibt.

Für einen sinnvollen Vergleich mit der Standardformel muss aber der Eigenkapitalbedarf zum Jahresende zugrunde gelegt werden, da in der Standardformel erwartete Gewinne (oder auch Verluste) nicht eingerechnet werden. In der nachfolgenden Darstellung sind daher die Ergebnisse der SCR-Berechnung der Standardformel den EK-Bedarfen des internen Modells zum Jahresende gegenübergestellt. ⁵

Obwohl bei der Konzeption des internen Modells versucht wurde, möglichst nahe an der Parametrisierung der Standardformel zu bleiben, ergeben sich doch einige bemerkenswerte Unterschiede:

• 1. Das Marktrisiko wurde insgesamt gut reproduziert. Die Korrelationsstruktur bei der Aggregation zum Gesamtbedarf in der Standardformel ist aber nicht gut nachbildbar.
• 2. Die Ausfallrisiken werden durch das interne Modell höher eingeschätzt als bei der Standardformel. Die Algorithmen der Standardformel sind hier nicht gut nachbildbar.
• 3. Die UW-Risiken können als vergleichsweise gut getroffen betrachtet werden, wenn man akzeptiert, dass eine 1:1 Abbildung kaum möglich ist.
• 4. Das diversifizierte BSCR und die immateriellen Risiken sind vergleichsweise gut reproduziert. Die Addition der EK-Bedarfe kann aber nicht wirklich reproduziert werden.

• 5. Das operationelle Risiko ist im internen Modell kleiner, da der etwas „günstigere“ Risikomatrix-Ansatz gewählt wurde. Die Addition des operationellen Risikos ist im internen Modell nicht reproduzierbar.
• 6. Trotz analoger Abschreibungsalgorithmen ergibt sich im internen Modell ein deutlich höherer Adjustierungseffekt durch aktive latente Steuern. Aus diesem Grund beobachtet man auch (sozusagen als Kompensation) einen Antidiversifikationseffekt.

Selbst wenn man also bei einem internen Modell zur Standardformel möglichst vergleichbare Parametrisierungen und Modellierungsansätze wählt, können die Ergebnisse nicht wirklich reproduziert werden. Dies liegt an den teilweise sehr realitätsfremden Algorithmen, insbesondere aber an den künstlich angesetzten (und somit nicht oder nur unter sehr unnatürlichen Annahmen reproduzierbaren) Korrelationsmatrizen bei der Aggregation zum Gesamtrisikobedarf, was sich sozusagen durch alle Risikomodule hindurchzieht.