Grundlegendes zum Chain Ladder-Verfahren
In der Praxis erfolgt die Schadenreservierung meist auf Grundlage so genannter Abwicklungsdreiecke, wobei zwischen Schadenzuwächsen und Schadenständen unterschieden wird. Im Abwicklungsdreieck werden die abzuwickelnden Schäden eines Anfalljahres zusammen mit den Abwicklungsdaten mehrerer Anfalljahre dargestellt. Die Regulierung der Schäden eines Anfalljahres kann sich dabei von der Entstehung im Anfalljahr bis zur abschließenden Abwicklung über mehrere Abwicklungsjahre erstrecken. Es wird angenommen, dass die Geschäftsjahre mit den Kalenderjahren übereinstimmen. Das Abwicklungsdreieck enthält dabei für jedes Anfalljahr und jedes Abwicklungsjahr die Gesamtheit aller geleisteten Zahlungen.
Formal beschreibt man die anfallenden Zahlungen durch eine Familie {Zi,k}i,k∈{0,1,…,n} von Zufallsvariablen. Zi,k definiert die Schadenzuwächse im (relativen) Abwicklungsjahr k für Schäden aus dem (relativen) Anfalljahr i. Die Zahlung Zi,k erfolgt somit im (relativen) Kalenderjahr i+k. Man geht davon aus, dass die Zuwächse für i+k ≤ n beobachtbar und für i+k > n nicht beobachtbar sind unter der Annahme, dass die Regulierung jedes Schadens im selbigen Anfalljahr oder innerhalb der n folgenden Kalenderjahre erfolgt. Die beobachtbaren Schadenzuwächse können dann in einem Abwicklungsdreieck {Zi,k}i+k ≤ n dargestellt werden. Werden die beobachtbaren Schadenzuwächse um die zukünftigen nicht beobachtbaren Schadenzuwächse ergänzt, erhält man das sogenannte Abwicklungsquadrat.
Beispiel:
Einem Versicherungsunternehmen liegen aus den letzten 6 Jahren folgende Informationen zu Schadenzahlungen aus der Sparte Kfz-Haftpflicht vor (in Mio. €):
| Abwicklungsjahr (Schadenzuwächse) | ||||||
|---|---|---|---|---|---|---|
| Anfalljahr | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 |
| 2003 | 383 | 531 | 299 | 230 | 183 | 51 |
| 2004 | 468 | 641 | 233 | 187 | 132 | |
| 2005 | 248 | 302 | 223 | 185 | ||
| 2006 | 267 | 306 | 253 | |||
| 2007 | 223 | 304 | ||||
| 2008 | 222 |
Zum Beispiel wurden für Schäden aus dem Anfalljahr 2006 noch im selben Jahr Schadenzahlungen von 267 Mio. Euro fällig. In den folgenden Abwicklungsjahren erfolgten dann Zahlungen in Höhe von 306 Mio. Euro (2007) bzw. 253 Mio. Euro (2008).
Anhand des obigen Abwicklungsdreieckes ist ein Abwicklungsmuster erkennbar: die bisher geleisteten Zahlungen im zweiten Abwicklungsjahr nach Eintritt des Schadens fallen am höchsten aus und nehmen dann in den Folgejahren langsam ab. Dabei ist dieser Effekt durch die gewählte Darstellungsform nicht deutlich erkennbar. Jedoch sind Trendstrukturen und Abwicklungsmuster wesentliche Indikatoren für die Höhe der zukünftigen Zahlungen und die dadurch erforderlichen Spätschadenreserven. Aus diesem Grund werden die absoluten Abwicklungsdreiecke (Basis: Kalenderjahre) fast immer als relative Abwicklungsdreiecke (Verzögerungen in Bezug auf die Anfall- bzw. Abwicklungsjahre) behandelt und man erhält das folgende Abwicklungsdreieck mit den nicht-kumulierten Zahlungen für obiges Beispiel:
| Abwicklungsjahr k (Schadenzuwächse) | ||||||
|---|---|---|---|---|---|---|
| Anfalljahr i | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 383 | 531 | 299 | 230 | 183 | 51 |
| 1 | 468 | 641 | 233 | 187 | 132 | |
| 2 | 248 | 302 | 223 | 185 | ||
| 3 | 267 | 306 | 253 | |||
| 4 | 223 | 304 | ||||
| 5 | 222 |
Dieses Abwicklungsdreieck enthält die beobachtbaren Schadenzuwächse in den relativen Abwicklungsjahren für die relativen Anfalljahre und bildet die Basis für alle weiteren Betrachtungen (engl.: run-off-triangle). i+k bezeichnet hier das relative Kalenderjahr, mit n = 5
Aufgrund dieser Darstellung befinden sich jetzt die letzten geleisteten Schadenszahlungen im Jahr 2008 für die Anfalljahre 2003 – 2008 auf der (gelb markierten) Hauptdiagonalen.
Um die Spätschadenreserve mit der Chain Ladder-Methode ermitteln zu können, benötigt man die Schadenstände
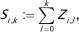
wobei vorausgesetzt sei, dass die Si,k ausschließlich positive Werte annehmen und (schwach) monoton wachsend in k sind. Die Schadenzuwächse Zi,k sind dann wie folgt gegeben:
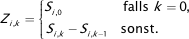
Die Größen Si,k bezeichnen dabei die kumulierten Jahresschäden, d.h. die im Anfalljahr i bis zum Abwicklungsjahr k saldierten (gemeldeten oder bezahlten) Schäden. Die Schadenzahlungen erfolgen dann in den Kalenderjahren q∈{i,…,i+k} . Wie bei den Schadenzuwächsen angenommen, sind auch die Schadenstände Si,k für i+k≤n beobachtbar und für i+k>n nicht beobachtbar. Auch die beobachtbaren Schadenstände lassen sich wie oben in einem Abwicklungsdreieck {Si,k}i+k≤n darstellen. Si,n bezeichnet dabei den Endschadenstand im Anfalljahr i und Si,n-i den letzten beobachtbaren Schadenstand. Die Endschadenstände sind mit Ausnahme des Anfalljahres i = 0 nicht beobachtbar. Letztendlich befinden sich auf der (gelb markierten) Diagonalen die aktuellen letzten Schadenstände.
Für die Schadenstände des Beispiels erhält man als kumulierte Jahres-Schäden:
| Abwicklungsjahr k (Schadenstände) | ||||||
|---|---|---|---|---|---|---|
| Anfalljahr i | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 383 | 914 | 1213 | 1443 | 1626 | 1677 |
| 1 | 468 | 1109 | 1342 | 1529 | 1661 | |
| 2 | 248 | 550 | 773 | 958 | ||
| 3 | 267 | 573 | 826 | |||
| 4 | 223 | 527 | ||||
| 5 | 222 |
Die Vervollständigung dieses Abwicklungsdreiecks zu einem Abwicklungsquadrat geschieht beim Chain Ladder-Verfahren über Abwicklungsfaktoren, die folgendermaßen definiert sind:
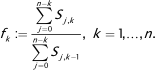
Sie stellen im Prinzip das gewichtete Verhältnis zwischen zwei benachbarten Spalten dar und beschreiben damit in gewisser Weise das mittlere Wachstum der Schadenstände in aufeinander folgenden Abwicklungsjahren. Die Auffüllung des Abwicklungsdreiecks geschieht nun durch sukzessive Multiplikation der Diagonalelemente Si,n-i mit den Abwicklungsfaktoren fn-i+1,…,fk mit i,k ∈ {0,1,…,n}, i+k ≥ n. Im obigen Beispiel erhält man so etwa
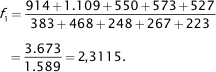
Die nachfolgende Graphik zeigt die gesamten Abwicklungsfaktoren in der unteren Zeile sowie die Vervollständigung des Abwicklungsdreiecks nach dem Chain Ladder-Verfahren (graue Felder).
| Abwicklungsjahr k (Schadenstände) | |||||||
|---|---|---|---|---|---|---|---|
| Anfalljahr i | 0 | 1 | 2 | 3 | 4 | 5 | benötige Reserve |
| 0 | 383 | 914 | 1213 | 1443 | 1626 | 1677 | - |
| 1 | 468 | 1109 | 1342 | 1529 | 1661 | 1713 | 52 |
| 2 | 248 | 550 | 773 | 958 | 1060 | 1093 | 135 |
| 3 | 267 | 573 | 826 | 975 | 1079 | 1113 | 287 |
| 4 | 223 | 527 | 696 | 822 | 909 | 937 | 410 |
| 5 | 222 | 513 | 678 | 800 | 885 | 913 | 691 |
| fk | - | 2,3115 | 1,3204 | 1,1809 | 1,1060 | 1,0314 | Summe: 1575 |
Die in der letzten Spalte des Abwicklungsdreiecks notierten Schadenstände heißen auch Ultimates. Die benötigte Reserve je Anfalljahr i ergibt sich jetzt aus der Differenz des Ultimates und des Diagonalelements in Zeile i (blaue Felder). Durch Saldierung aller Einzelreserven ergibt sich die benötigte Gesamtreserve.
Besonderheiten in der Delegierten Verordnung
Aufgrund der marktnahen Bewertung aller Bilanzpositionen unter Solvency II sind die in den Folgejahren anfallenden Zahlungen grundsätzlich mit den von EIOPA vorgegebenen Zinsstrukturkurven (risikolos, Zinsanstieg, Zinsrückgang) zu diskontieren. Dies ist bei der Anwendung des Chain Ladder-Verfahrens zu berücksichtigen. Die Ultimates entsprechen damit den Barwerten des aus der Abwicklung resultierenden Zahlungsstroms. Allerdings geht durch die nur auf die Diagonale in gleicher Weise wirkende Diskontierung die zeitliche Vergleichbarkeit in der Abwicklung verloren. Es bietet sich daher an, das Chain Ladder-Verfahren zunächst ohne Diskontierung durchzuführen und anschließend die aus dem Abwicklungsquadrat ermittelten Zuwächse zu diskontieren. Die Einzelreserven und die Gesamtreserve können abschließend wie oben errechnet werden
Für die einzelnen Geschäftsfelder des versicherungstechnischen Risikos wird dabei ein Zeitraum zu Grunde gelegt, der für eine vollständige Abwicklung benötigt wird. Reichen die Daten des Versicherungsunternehmens hier nicht aus, sind statistisch motivierte Verlängerungen der Abwicklungsdreiecke vorzunehmen (sog. Nachläufe auf der Basis nichtlinearer Regressionsansätze).
Der GDV hat in Zusammenarbeit mit der Deutschen Aktuarvereinigung und der TU Dresden im Jahr 2008 eine umfängliche Broschüre mit dem Titel „Methoden zur Schätzung von Schaden- und Prämienrückstellungen“ herausgegeben, die auf die genannten Punkte sehr ausführlich eingeht.