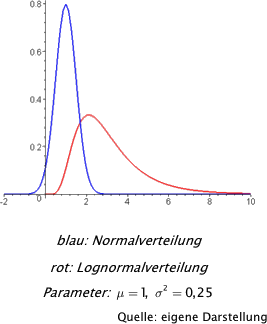
Statistische Grundlagen
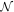 (µ,σ²) ist durch die beiden Parameter µ ∈ ℝ (Erwartungswert) und σ² ∈ ℝ+ := {x ∈ ℝ | x > 0} (Varianz) charakterisiert. Die Größe σ = √σ² heißt in der Statistik auch Standardabweichung oder Streuung. Bezeichnet m = E(X) den Erwartungswert von X und s² = Var(X) die Varianz von X, so besteht folgende Beziehung zwischen diesen Größen und den Parametern µ und σ²:
(µ,σ²) ist durch die beiden Parameter µ ∈ ℝ (Erwartungswert) und σ² ∈ ℝ+ := {x ∈ ℝ | x > 0} (Varianz) charakterisiert. Die Größe σ = √σ² heißt in der Statistik auch Standardabweichung oder Streuung. Bezeichnet m = E(X) den Erwartungswert von X und s² = Var(X) die Varianz von X, so besteht folgende Beziehung zwischen diesen Größen und den Parametern µ und σ²:
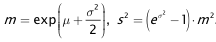
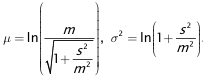
β = P(X ≤ LNβ) = P(ln(X) ≤ ln(LNβ))
= P(ln(X) ≤ Nβ),
Nβ = ln(LNβ) bzw. LNβ = exp(Nβ)
ergibt. Das allgemeine β-Quantil Nβ(µ,σ²) der Normalverteilung steht mit dem β-Quantil Nβ(0,1) der Standardnormalverteilung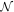 (0,1) in folgendem Zusammenhang:
(0,1) in folgendem Zusammenhang:
Nβ(µ,σ²) = µ + σ · Nβ(0,1).
Damit ist das allgemeine β-Quantil der Lognormalverteilung gegeben durchLNβ(µ,σ²) =exp(Nβ(µ,σ²)) = exp(µ + σ · Nβ(0,1)).
Verwendung in QIS 5
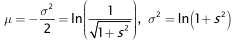
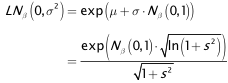
Revised Technical Specifications und technische Spezifikationen für die Übergangszeit
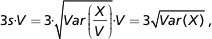
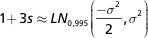
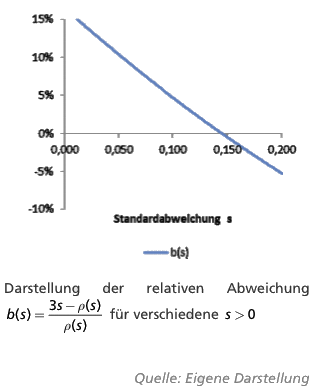
ρ(s) ≈ 3s, für alle s ∈ I.
Die nachstehende Abbildung zeigt den relativen Approximationsfehler für sinnvoll erscheinende Wahlen von s. Man beachte, dass die Approximation den zu approximierenden Wert im Falle positiver Werte übersteigt. Berücksichtigt man, dass ein verteilungsfreier Ansatz keine Grundlage zur Bestimmung eines Sicherheits- bzw. Risikoniveaus liefern kann, und wird gleichzeitig die Einhaltung eines hypothetischen Sicherheitsniveaus strikt gefordert, so liegt es nahe, auch weiterhin von einer nun aber still gestellten Lognormalverteilungsannahme auszugehen oder aber an einer anderen Stelle ein geeignetes Verteilungsmodell zu unterlegen – obgleich die handlichere Approximationsformel bei der Berechnung des Solvenzkapitals zur Anwendung kommt.Herangezogene technische Spezifikationen
CEIOPS. QIS5 Technical Specifications. 2010. URL: https://eiopa.europa.eu/fileadmin/tx_dam/files/consultations/QIS/QIS5/QIS5-technical_specifications_20100706.pdf EIOPA. Revised Technical Specifications for the Solvency II valuation and Solvency Capital Requirements calculations (Part I). EIOPA-DOC-12/467. 2012. URL: https://eiopa.europa.eu/fileadmin/tx_dam/files/consultations/QIS/Preparatory_forthcoming_assessments/A_-Revised_Technical_Specifications_for_the_Solvency_II_valuation_and_Solvency_Capital_Requirements_calculations__Part_I.pdf EIOPA. Technical Specification for the Preparatory Phase (Part I). EIOPA-14/209. 2014. URL: https://eiopa.europa.eu/fileadmin/tx_dam/files/publications/technical_specifications/A_-Technical_Specification_for_the_Preparatory_Phase__Part_I.pdf